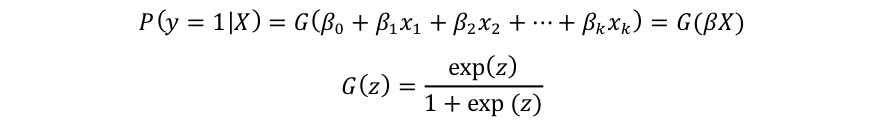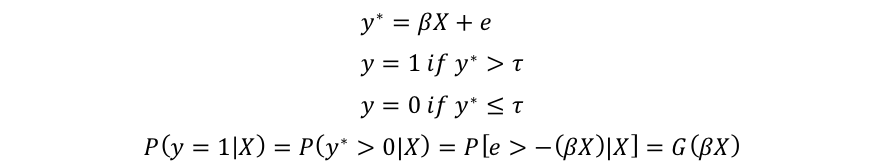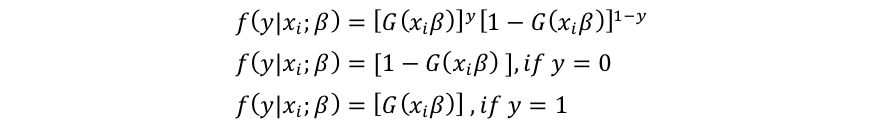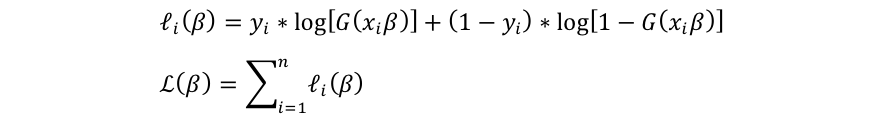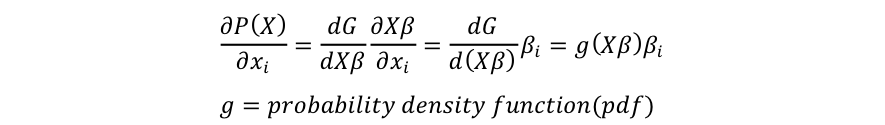最近はお仕事で使いそうな分析を復習する日々です。
ざっくり調べた感じだとネット広告では重回帰・ロジスティック回帰・マルコフ連鎖辺りを使う機会が多そうなのでその辺を重点的にやってます。
日本語でアウトプットしておかないととっさに説明とか出来なさそうなので、練習も兼ねてここで解説しようかと。まぁロクな解説になってないですがw
まずある特定の事象を予測したいとします。例えば、25歳・修士卒・資格無し・文系の人が仕事を得ることが出来るか否か?といった事象を予測したいとします。
知りたい事象は仕事の有無なので、これを表すのにバイナリの変数を使います。
つまり、y=1なら就職しており、y=0なら就職をしていない、となります。
そして何かを予測する時に絶対的な答えを求めることは不毛であるので、ある人物が就職できる確率を求めることにします。
P(y=1 | X) = P(y=1 | x1, x2, x3,…, xk)
P(y=1)で就職している確率を表します。これに|Xを付け加えてP(y=1|X)にすると、条件Xが与えられた時に就職している確率を示すことになります。
条件Xとは上で挙げた、年齢・教育・資格・専門等々といった要素です。これらの要素が全部でk個あると推測すると、条件Xの中にはx1~xkまでのk個の要素が入っているという事になります。
線形確率モデル(LPM)を使うならばこのまま単純にOLSで回帰分析をすれば良いのですが、LPMには幾つかの欠点があります。
LPMはそれぞれの要因(例:年齢・教育・資格・専門)が事象の確率に線形で影響すると考えます。つまり、年齢が20から21になった時の影響と、50から51になった時の影響が同じであるということを前提にします。
教育では初等教育の1年と高等教育の1年では労働市場での評価は明らかに違うためにモデルの精度に疑問が生まれます。
また、LPMでは線形であるがゆえに0~1の間に予測されるはずである確率が負の値を取ったり1を超えたりしてしまいます。
Loogitモデルではこれらの欠点を補うためにlogistic function (G)を導入します。
回帰モデルをGでlogitモデルにしてしまうことによって、極端な事象が起こり難い様に成ります。
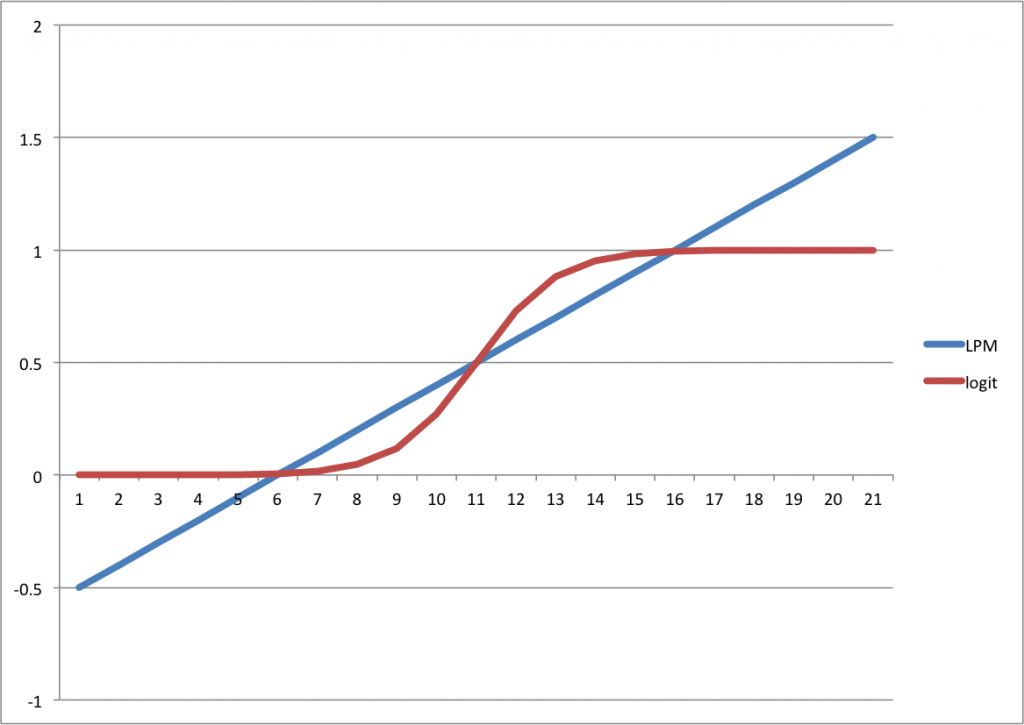
LPMとlogitを単純に比較すると下の図のようになります。
LPMでは要素が極端に大きいか小さいと確率yが0-1の範囲を超えてしまいます。一方でlogitの場合ではちゃんとその範囲に収まっています。
さて、y=1になる(つまり、就職出来る)確率と単純に言っていますが、どんな状態の時にy=1となるのでしょうか?
logitモデルではそのメカニズムにunobserved latent variable(y*)を用いています。
これは見えない点数みたいなもので、就職の例で考えれば就職スコアみたいなものです。このスコアが一定以上であれば職が見つかり、一定以下であれば見つからないといった感じの物です。
このスコアは当然要素Xによって左右されるのでβXで表され、eは誤差項になります。
もしy*がt(判別値)よりも大きければy=1で、そうでなければy=0となります。多くの場合では判別値には0が用いられます。
y=1になる確率はy*が判別値(ここでは0)よりも大きくなる確率と同等になり、G(βX)で求める事が出来ます。
logit モデルを扱う場合、大体興味がある部分はある要素xが事象yに対してどの程度の影響があるか?という部分です。つまり、y*そのものはあまり興味のある対象ではないわけです。
そしてlogitモデルを推定した場合残念ながらβはxがy*に与える影響を示してしまうため、結果を簡単に解釈することが出来ません。ただ、これに関しては後回しにします。
・最尤法で推定
さて、推定とサクッと言いましたが一体どのように推定するのでしょう?
明らかに線形回帰の出番ではありません。非線形回帰で求めることも出来るのですが、簡単なものは最尤法(maximum likelyhood estimation: MLE)でしょう。
yの確率密度関数は以下の様に定義が可能です。
基本的にはある要素の値が与えられた時の結果yが起こる確率を与えてくれる式だと考えればOKです。
結果yの値によって確率が
もし与えられた条件での結果がy=1だったとすれば、それが起きる確率がどの程度であったのかを教えてくれるわけです。
もうちょい具体的に言えば、25歳で修士で文系で資格が無い人が内定を取ったとしたら、内定を取れる確率がどの程度であったのかを教えてくれるわけです。
データを取ってしまえばどんな要素を持っている人が職を得たか得られなかったかが解るため、yとxは埋まります。つまり、βの値次第でこの式が算出する確率は変わることになります。
最尤法とは、実際に起った事象は最も起こりやすかったから起きたと想定する事に基づいています。最も起こりやすいとは確率が最も高い = f(y|x;β)の値が最も高いということになります。
よって、最尤法に基づけば、f(y|x;β)が一番大きくなるようなβを探せば良いということになります。(なぜならそのβがデータで起きた事象を最も起こりやすかったから起きたと解釈させてくれるからです。)
さて、この式を計算しやすくするためにlogを取ってlog likelyhood functionにします。
そしてこの2つ目の式を最大化させるβを求めればlogitモデルを推定することができます。
・推定結果をどう理解するか?
さて影響を知りたい変数xが連続である時、βはy*に対する影響なので、yに対する影響を知るためには偏微分に頼ることになります。
知りたいのは確率Pに対してある変数x_iがどの程度の影響を与えるか?なので、確率関数P(y=1 | X)=P(X)をx_iで偏微分します。
Gはcumulative distribution functionなので、微分をするとprobability density functionになります。
x_iが変化した時の確率への影響はβ_iにpdfを掛けた値になります。つまり、影響は他の要素Xの値次第で変わってしまうと言う事になります。
logitモデルを使う事の大きなコストとして、この影響が変わってしまう点が挙げられます。
基本的にはそれぞれの要素に興味のある値を投入して、その時の効果を測定するという方法があります。これはある特定の人が就職できるか否かを予測したい時なんかに使えます。
また全ての変数に平均値を代入して効果を測定するParial Effect on Average(PEA)という方法もあります。
また、偏微分をすべての値で行なってその結果を平均するというAverage Partial Effectという方法も存在しており、これら3つは用途によって使い分けられています。計量経済学では基本的にはPEAを使用して、予測する際には興味のある値を投入しています。
ダミー変数をモデルに投入している場合、PEAもAPEも適していません。例えば性別を投入した場合、平均値は0.5になってしまいその数値自体に意味合いが持てなくなるからです。
よってダミー変数以外に平均値や興味のある値を代入し、ダミー変数が1の場合と0の場合を計算して差し引く事によってそのダミー変数の影響を調べることが出来ます。
・R^2系
モデルの精度を知りたいときにはLPMであればR^2を使えば良いのですが、logitでは使うことができません。1つの代替案としてあるのがPercent correctly Predictedというものです。
推定したモデルにデータを投入してみてyを推測させ、それを実際の結果と比較し、推測が正解している割合を求めるというものです。
モデルは推測するときにyの期待値を出すので、0か1といった値は出力されません。よって推測された値(yの期待値)が判別値より上か下かで見ることになります。一番シンプルな判別値は0.5で、0.5より大きければ1であると見なし、それ以下は0と見なします。
この様に結果を1か0に振り分け、実際の値と比較するわけです。
しかし、この方法ではデータセットの結果の割合に気をつけなければいけません。
もし元々のデータセットの中でy=1の割合が90%であった場合、期待値はかなり高めに偏ってしまうため、0.5以下は殆ど出力されません。しかし、90%が1なので全体の正解率だけを見てしまうとモデルの精度がそんなに悪いものでは無いと判断することが出来てしまいます。
このようなケースではデータセットでyの平均値を計算してその値を判別値に使います。ここでは0.9なので0.9を判別値に使用します。これによってy=1を推測するときの精度が落ちてしまうものの、y=0の時の精度を大きく上昇させることができます。
また、全ての判別値を試して、推測されたyの平均と実際のyの平均が近似する様な判別値を選択するという方法もあります。
他にもpseudo R^2とかもあるのですが、説明は省略します。
・検定周り(t and F test)
検定は標準偏差が手に入れば普通のt検定が使用出来ます。(ただ、標準偏差の計算がかなりダルい・・・)
F-testのような検定も存在しており、Likelyhood ratio testというものが使用可能です。
F-testではR^2が変数の有無で変化するか否かを見るわけですが、Likelyhood ratio test では変数が全て入ったモデルのlog likelyhoodから変数が制限されているモデルのlog likelyhoodを差し引いた値を2倍したものをLikelyhood Ratio(LR)として使用します。
このLRは取り除いた変数の数を自由度として持つchi-sq分布を持つということが分かっているのでchi-sq testを行なってF-testのような検定を行うことができます。
最初logitモデルを勉強した時はヤケに胡散臭いなと思ったものです。 最近やっと確率分布の事とかが解ってきたためにこういう処置は必ず必要だなと思うようになりました。
事象が本当に確率で分布するという認識がなければ使おうとしない手法なのだと思います。計量経済学ではlogitではなくてprobitを使うわけなんですが、この辺はどれを選択してゆけばいいのかはまだちょっと解りません。
理系で分析してた方はlogitを好む傾向にあるなというイメージがありますが・・・どーなんでしょ。
恐らく実務で消費データに対して統計分析を使う場合って、ユーザーの特徴と購入したか否かみたいなデータセットを自分で作って、どんな施策とか行動特徴が購買に繋がってるかを見つける事になると思うのでlogitモデルはかなり重要な部分を占めるのではないかな?と思います。
ただ、同じ事を他の手法でも間違いなく可能なわけです。ランダムフォレストとかまさにその1つだと思いますし、サポートベクターマシンだって使えると思います。
そういった代替手段がある中でlogitモデルを選択する理由みたいなものを把握してゆかないといけないはずなんですが、そのへんはまだまだ勉強不足ですね・・・
なんとなく思うのはパネルデータへの対応とかはlogitモデルのほうが楽なのかなと。ただパネルを使う機会が果たしてあるのやら無いのやら・・・
ちなみに今回の記事は下の教科書を参考にしました。